歩行経路と距離についての一考察 ― 2014年05月22日
「認知症やボケの防止には身体を動かしながら脳を積極的に働かせるなど、二重タスクによるトレーニングを行うのが良い」ということがあるテレビ番組で紹介されていました。
そこで、散歩しながら「歩行経路によって歩行距離がどう変わるか」について考えてみました。その結果を整理し、少々気取ったタイトルにしてブログにアップしようと思います。仰々しいタイトルの割には内容が単純でつまらないものだと思いますが、興味がありましたら一緒に考えてみてください。
~ ~ ~ ~ ~
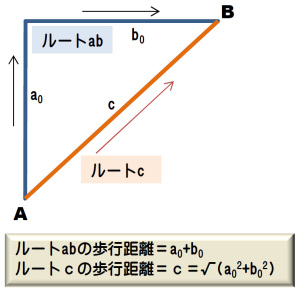
次の図に示した「A地点」から「B地点」まで歩く場合、“ルートab”の経路よりも“ルートc”の経路のほうがショートカットしている分だけ距離が短いということは図を見れば直感的に分かりますよね。
そこで、散歩しながら「歩行経路によって歩行距離がどう変わるか」について考えてみました。その結果を整理し、少々気取ったタイトルにしてブログにアップしようと思います。仰々しいタイトルの割には内容が単純でつまらないものだと思いますが、興味がありましたら一緒に考えてみてください。
~ ~ ~ ~ ~
次の図に示した「A地点」から「B地点」まで歩く場合、“ルートab”の経路よりも“ルートc”の経路のほうがショートカットしている分だけ距離が短いということは図を見れば直感的に分かりますよね。
直感だけでなく、数式で考えてもルートcの歩行距離が短いことが理解できます。
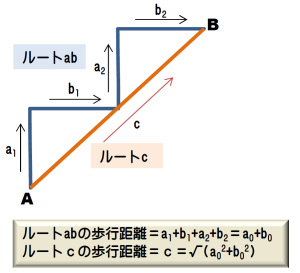
では、折れ曲がる回数を増やした次の場合はどうでしょうか。
では、折れ曲がる回数を増やした次の場合はどうでしょうか。
やはり、ルートcの経路のほうが短いと思えますよね。
では折れ曲がる回数をさらに増やした次の場合はどうでしょうか。
では折れ曲がる回数をさらに増やした次の場合はどうでしょうか。
最初の図の経路に比べ、折れ曲がる回数を多くしたので、マクロ視するとルートabの経路はルートcの経路に近づいているのが分かります。それなら、最初の図のルートabよりもこの図のルートabのほうが歩く距離が短くなっているのでしょうか。
上図のルートabの経路で歩く距離を数式で表すと、図の下に示したようになります。つまり、最初の図におけるルートabと変わらないんです。不思議ですよね。
では、もっと極端な場合を考えてみましょう。折れ曲がる回数を“無限に近い数”にした場合はどうなるのかというと、数式の項が無限に近く増えるだけで、トータルの距離は変わらないんです。
でも、図で表すと折れ曲がりのギザギザが非常に細かくなり、概観するとルートcと重なっているように見えます。だったら、歩く距離もルートcと同じになっても良いように思えますよね。 う~ん、謎です。
この謎を解くには、細かく巻いたコイルバネを例にとって考えるのが良いかもしれません。
縮んだコイルバネを遠くから見れば一本の短い線にしか見えないのですが、

バネを延ばすと、芯線はとても長いんです。

つまり、縮めたバネは短く見えるのですが、芯線に沿って進むとするなら、その距離は芯線の長さに等しいのです。
バネの理屈を3番目の図に置き換えて考えてみましょう。歩く経路のギザギザを多くするとルートcに近くなっているように見える(縮んだバネの長さ)のですが、進む方向が縦と横の組み合わせ(バネの芯線に沿った進み方)である限り、歩く距離はルートab(芯線の長さ)と同じということになるんですね。
これでお分かりでしょうか。
~ ~ ~ ~ ~
以上は、「碁盤の目のように整備された道路を歩く場合、何回も折れ曲がりながら進むのと、最初の図に示したルートabのように進むのでは歩行距離が異なるのか?」という疑問について歩きながら考えたことです。
考えた結果は、以下のように要約されます。
●折れ曲がる回数を増やすと、見た目には斜めに進んだ経路に近づくので歩行距離が短く
なるように思えるが、進む方向が縦と横の組み合わせである限り短くはならない。
●歩行距離が短くなるのは、進む方向を斜めにした場合である。
説明があまり上手くないので、理解しにくかったかもしれませんね。 m(_ _)m